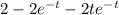Question

Find inverse laplace transform for x(s) = (2)/(s(s+1)^2)

Answer 1

x(t)=
`2-2e^(-t)-2te^(-t)`

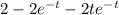
Explanation:

The function x(s) = (2)/(s(s+1)^2) can be expressed as partial fractions:

X(s)=
`(2)/(s(s+1)^2)=(A)/(s)+(B)/(s+1)+(C)/((s+1)^2)`

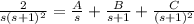
2=A·(s+1)²+B·s·(s+1)+C·s

2=A·(s²+2s+1)+B·(s²+s)+C·s

2=A·s²+2sA+A+B·s²+Bs+C·s

2=s²(A+B)+s(2A+B+C)+A

So we can find the values of A, B and C by solving these equations:

A+B=0 ⇒ 2+B=0 ⇒ B= -2

2A+B+C=0 ⇒ 2·2+(-2)+C=0 ⇒ C= -2

A=2

So X(s) is expressed as:

X(s)=
`(2)/(s)+(-2)/(s+1)+(-2)/((s+1)^2)`

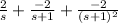
Using the inverse laplace transform tables we obtain x(t):

ℒ⁻¹{X(s)}=ℒ⁻¹{
`(2)/(s)+(-2)/(s+1)+(-2)/((s+1)^2)`}

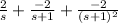ℒ⁻¹{X(s)}=ℒ⁻¹{
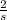`(2)/(s)`}+ℒ⁻¹{
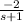`(-2)/(s+1)`}+ℒ⁻¹{
`(-2)/((s+1)^2)`}

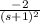x(t)=
`2-2e^(-t)-2te^(-t)`