Answer:
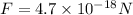
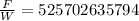
Step-by-step explanation:
The acceleration experimented by the electron can be calculated using the formula
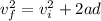 , so we have:
, so we have:
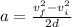
The magnitude of of the force exerted on the electron can be then obtained using Newton's 2nd Law F=ma.
Putting all together we have:

And using our values (and that 4.2cm are 0.042m):
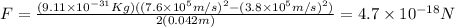
Then we compare this force with the weight of the electron:

So this force is 525702635794 times larger than the weight of the electron.