Answer:
69.92°F
Explanation:
Given:
Initial temperature ( i.e at time, t = 0) = 40°F
Temperature of the room = 70°F
Temperature after 10 minutes ( i.e at time t = 10 ) = 48°F
Now, from Newton's law of cooling
T'(t) = k(A - T(t))
T(t) temperature after time t
T'(t) =
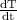
here, A is the room temperature
thus,
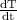 = k(70 - T)
= k(70 - T)
or
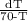 = kdt
= kdt
on solving the differential equation, we get
T =
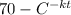 ............(1)
............(1)
Now from the boundary conditions,
i.e at time, t = 0; T = 40°F
we get,
40 =
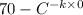
or
C = 30
and,
at time, t = 10; T = 48°F
thus,
48 =
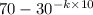
or
k =
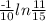
or
k = 0.03
Therefore,
for t = 25
from 1 we have
T =
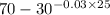
or
T = 70 - 0.0780
or
T = 69.92°F