Question

Suppose a cold beer at 40°F is placed into a warm room at 70°F. Suppose 10 minutes later, the temperature of the beer is 48°F. Use Newton's law of cooling to find the temperature 25 minutes after the beer was placed into the room.

Answer 1

69.92°F

Explanation:

Given:

Initial temperature ( i.e at time, t = 0) = 40°F

Temperature of the room = 70°F

Temperature after 10 minutes ( i.e at time t = 10 ) = 48°F

Now, from Newton's law of cooling

T'(t) = k(A - T(t))

T(t) temperature after time t

T'(t) =
`\frac{\textup{dT}}{\textup{dt}}`

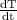
here, A is the room temperature

thus,

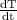`\frac{\textup{dT}}{\textup{dt}}` = k(70 - T)

or

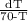`\frac{\textup{dT}}{\textup{70-T}}` = kdt

on solving the differential equation, we get

T =
`70-C^(-kt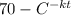)` ............(1)

Now from the boundary conditions,

i.e at time, t = 0; T = 40°F

we get,

40 =
`70-C^(-k*0)`

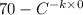
or

C = 30

and,

at time, t = 10; T = 48°F

thus,

48 =
`70-30^(-k*10)`

or

k =
`\frac{\textup{-1}}{\textup{10}}ln(11)/(15)`

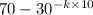
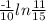
or

k = 0.03

Therefore,

for t = 25

from 1 we have

T =
`70-30^(-0.03*25)`

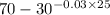
or

T = 70 - 0.0780

or

T = 69.92°F