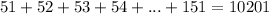Answer:
The sum of
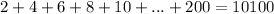
The sum of
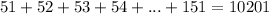
Explanation:
(a) To find the sum of
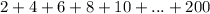 , take the first and the last number 2 + 200 = 202.
, take the first and the last number 2 + 200 = 202.
Now that those are accounted for, take the next smallest and largest numbers available: 4 + 198 = 202.
Continuing, 6 + 196 = 202
This repeats 50 times until reaching 50 + 152 = 202.
Since 202 repeats 50 times, the desired sum is 50 x 202 = 10100
Therefore
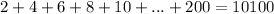
To check the result we can use the formula to sum of the first n even numbers:
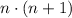
where n in our case is 100 because

so

(b) To find the sum of
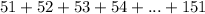 , do the same in point (a)
, do the same in point (a)
51 + 151 = 202
52 + 150 = 202
53 + 149 = 202
Note that there are (151 - 51 + 1 ) = 101 terms
so the sum will be
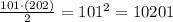
Therefore