Answer:
the value of k is 6 and 12.
Explanation:
The differential equation is y" – 18y' + 72y = 0.
A solution of this differential equation is
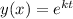
The first derivative is
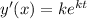
The second derivative is
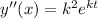
Substituting these values in the given DE
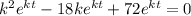
Factor out the GCF
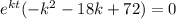
The function
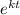 can never be zero. Hence, we have
can never be zero. Hence, we have
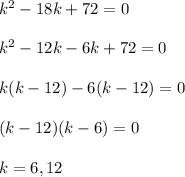
Therefore, the value of k is 6 and 12.
Smaller value = 6
Larger value = 12