Question

Find the two values of k for which y(x) = ekt is a solution of the differential equation y" – 18y' + 72y = 0. smaller value = larger value = Preview Preview

Answer 1

the value of k is 6 and 12.

Explanation:

The differential equation is y" – 18y' + 72y = 0.

A solution of this differential equation is

`y(x)=e^(kt)`

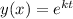
The first derivative is

`y'(x)=ke^(kt)`

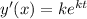
The second derivative is

`y''(x)=k^2e^(kt)`

Substituting these values in the given DE

`k^2e^(kt)-18ke^(kt)+72e^(kt)=0`

Factor out the GCF

`e^(kt)(-k^2-18k+72)=0`

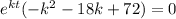
The function
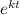`e^(kt)` can never be zero. Hence, we have

`k^2-18k+72=0\\\\k^2-12k-6k+72=0\\\\k(k-12)-6(k-12)=0\\\\(k-12)(k-6)=0\\\\k=6,12`

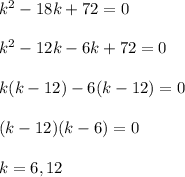
Therefore, the value of k is 6 and 12.

Smaller value = 6

Larger value = 12