Answer:
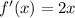
Explanation:
To Find :Find the derivative of the function by using the Product Rule. Simplify your answer. f(x) = (x - 3)(x + 3)
Solution :
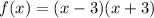
We will use chain rule of product
Formula :
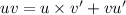
=
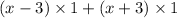
=
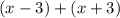
=
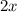
So,
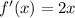
Hence the derivative of the function by using the Product Rule is 2x