Question

Find the derivative of the function by using the Product Rule. Simplify your answer. f(x) = (x - 3)(x + 3)

Answer 1

`f'(x)=2x`

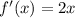
Explanation:

To Find :Find the derivative of the function by using the Product Rule. Simplify your answer. f(x) = (x - 3)(x + 3)

Solution :

`f(x) = (x - 3)(x + 3)`

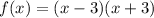
We will use chain rule of product

Formula :
`uv=u * v' +v \tyimes u'`

=
`(x-3) * 1+(x+3) * 1`

=
`(x-3)+(x+3)`

=
`2x`

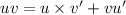
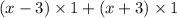
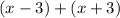
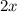
So,
`f'(x)=2x`

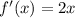
Hence the derivative of the function by using the Product Rule is 2x

Answer 2

`f'(x)=2x`

Explanation:

Given : Function
`f(x)=(x-3)(x+3)`

To find : The derivative of the function by using the Product Rule ?

Solution :

The product rule of derivative is

`(d)/(dx)(u\cdot v)=uv'+vu'`

Here, u=x-3 and v=x+3

`(d)/(dx)((x-3)\cdot (x+3))=(x-3)(d)/(dx)(x+3)+(x+3)(d)/(dx)(x-3)`

`(d)/(dx)((x-3)\cdot (x+3))=(x-3)1+(x+3)1`

`(d)/(dx)((x-3)\cdot (x+3))=x-3+x+3`

`(d)/(dx)((x-3)\cdot (x+3))=2x`

Therefore,
`f'(x)=2x`