Answer:
x-intercept and y-intercept of the given line is
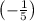 and
and

Solution:
The equation of the line is
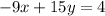
Simplifying this we get,
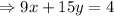


The slope of the line is (9/15), so the slope of the line perpendicular to this will be

Let us assume that the y intercept is b, so the equation is

Now, as that line passes through (-2,-3), hence using this point we get,
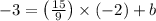
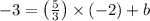
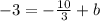
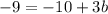


So the equation will be,
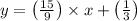
Now to find x intercept y =0, Hence,
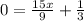
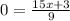
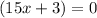
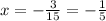
To find y intercept x = 0, Hence,

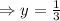
So, x intercept is
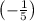 and y intercept is
and y intercept is
