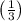Question

A line passes through (-2,-3) and is perpendicular to the line -9x+15y=4. Find it’s x-intercept and y-intercept.

Answer 1

x-intercept and y-intercept of the given line is
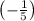`\left(-(1)/(5)\right)` and
`\left((1)/(3)\right)`

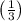
Solution:

The equation of the line is
`-9x+15y=4`

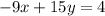
Simplifying this we get,

`\Rightarrow 9x+15y=4`

`\Rightarrow 15y =9x+4`

`\Rightarrow y=\left((9 x)/(15)\right)+\left((4)/(15)\right)`

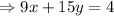
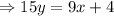
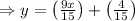
The slope of the line is (9/15), so the slope of the line perpendicular to this will be
`(15)/(9)`

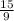
Let us assume that the y intercept is b, so the equation is
`y = mx + b`

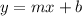
Now, as that line passes through (-2,-3), hence using this point we get,

`-3=\left((15)/(9)\right) *(-2)+b`

`-3=\left((5)/(3)\right) *(-2)+b`

`-3=-(10)/(3)+b`

`-9=-10+3 b`

`3 b=1`

`b=\left((1)/(3)\right)`

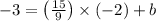
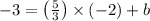
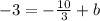
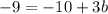
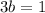
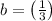
So the equation will be,

`y=\left((15)/(9)\right) * x+\left((1)/(3)\right)`

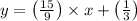
Now to find x intercept y =0, Hence,

`0=(15 x)/(9)+(1)/(3)`

`0=(15 x+3)/(9)`

`(15 x+3)=0`

`x=-(3)/(15)=-(1)/(5)`

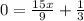
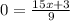
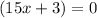
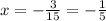
To find y intercept x = 0, Hence,

`y={((15)/(9)})*0+{((1)/(3)})`

`\Rightarrow y=(1)/(3)`

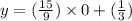
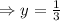
So, x intercept is
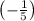`\left(-(1)/(5)\right)` and y intercept is
`\left((1)/(3)\right)`