Answer:
[122.23, 137.77]
Explanation:
In order to do this, we will be using the two sample z-statistic given by the formula
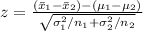
where
 = the sample mean strength for the specimens cured at 130°C
= the sample mean strength for the specimens cured at 130°C
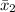 = the sample mean strength for the specimens cured at 150°C
= the sample mean strength for the specimens cured at 150°C
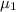 = the population mean strength for the specimens cured at 130°C (μX)
= the population mean strength for the specimens cured at 130°C (μX)
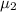 = the population mean strength for the specimens cured at 150°C (μY)
= the population mean strength for the specimens cured at 150°C (μY)
 = the sample standard deviation for the specimens cured at 130°C
= the sample standard deviation for the specimens cured at 130°C
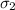 = the sample standard deviation for the specimens cured at 150°C
= the sample standard deviation for the specimens cured at 150°C
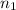 = the sample size for the specimens cured at 130°C
= the sample size for the specimens cured at 130°C
 = the sample size for the specimens cured at 150°C
= the sample size for the specimens cured at 150°C
z = 1.96, the z-score for a 95% confidence interval
Replacing values we have
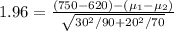
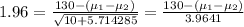
So, the 95% confidence interval for μX- μY =
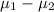 is the interval
is the interval
[130 - 1.96*3.9641, 130 +1.96*3.9641] = [122.23, 137.77] rounded to two decimal places.