Answer:
x =
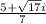
Explanation:
7
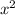 - 10
- 10
 = -6
= -6
All equations of the form
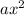 +
+
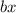 + x = 0 0 can be solved using the quadratic formula:
+ x = 0 0 can be solved using the quadratic formula:
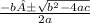 . The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.
. The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.
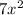 - 10
- 10
 = -6
= -6
Add 6 to both sides of the equation.
7
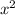 - 10
- 10
 - (-6) = -6 - (-6)
- (-6) = -6 - (-6)
Subtracting −6 from itself leaves 0.
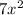 - 10
- 10
 + 6 = 0
+ 6 = 0
This equation is in standard form:
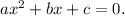 Substitute 7 for a, −10 for b, and 6 for c in the quadratic formula,
Substitute 7 for a, −10 for b, and 6 for c in the quadratic formula,
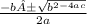
 =
=
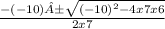
Square −10.
 =
=
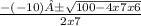
Multiply −4 times 7
 =
=

Multiply −28 times 6
 =
=
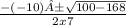
Add 100 to −168
 =
=
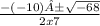
Take the square root of −68.
 =
=
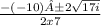
The opposite of −10 is 10.
 =
=
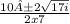
Multiply 2 times 7.
 =
=
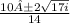
Now solve the equation
 =
=
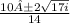 when ± is plus. Add 10 to
when ± is plus. Add 10 to
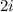
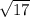 .
.
 =
=

Divide 10 +
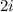
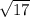 by 14
by 14
 =
=
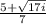
Now solve the equation
 =
=
 when ± is minus. Subtract
when ± is minus. Subtract
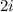
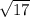 from 10.
from 10.
 =
=

Divide 10 -
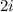
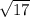 by 14
by 14
 =
=
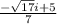
The equation is now solved.
 =
=
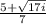
Hope it helps and have a great day! =D