Question

Which line has an equation of in slope-intercept form? a line passing through the points (1, 9) and (3, 19) a line passing through the points (2, –14) and (4, –24) a line passing through the points (1, 1) and (3, 11) a line passing through the points (2, –6) and (4, –16)

Answer 1

a line passing through the points (2, -6) and (4, -16)

Explanation:

Answer 2

Answer: Hi!

If you have a function y(x) = ax + b, where the slope is the number a and b is the x-axis intercept, whe can find the slope in the next way

`a = (y(x2) - y(x1))/(x2 - x1)`

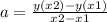
where x2 and x1 are different numbers.

now we know that our line passes through the points:

A) (1, 9) and (3, 19) (where the notation stands for (x, y))

we can find the slope as
`a = (19 - 9)/(3 - 1) = (10)/(2) = 5`

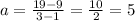
then the slope of this line is equal to 5, and we now need to finde the intercept b.

y(x) = 5x + b

we can repalace one of the pairs in the equation and then find b. for example the pair (1, 9)

9 = 5*1 + b

b = 9-5 = 4

then our line is: y = 5x + 4

B) (2, –14) and (4, –24)

The slope is
`a = (-24 + 14)/(4 - 2) = (-10)/(2)  = -5`

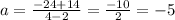
now we need to find the intercept, we do the same as before:

y = -5x + b

-14 = -5*2 + b

b = -14 + 10 = -4

then our equation is y = -5x - 4

C) (1, 1) and (3, 11)

We do the same procedure as before:

slope:
`a = (11 -1)/(3 -1) = (10)/(2) = 5`

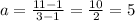
now for the intercept:

y = 5x + b

1 = 5*1 + b

b = 1 - 5 = -4

then our line is y = 5x - 4

D) (2, –6) and (4, –16)

The slope is
`a = (-16 + 6)/(4 - 2) = -5`

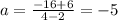
now we need to find the value of the intercept:

y = -5x + b

-6 = -5*2 + b

b = -6 + 10 = 4

then our line is y = -5x + 4