Answer: 0.923
Explanation:
Let A be the event an Internet user posts photos that they have taken themselves, and B be the event an Internet user posts videos that they have taken themselves.
Pew Research Center finds that
P(A)=0.52 P(b)=0.26, and P(A or B)=0.54.
To find : P(A|B)
Since ,
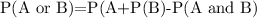
i.e.
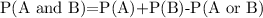
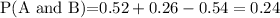
Now, using conditional probability formula ,

Hence, the conditional probability that an Internet user posts photos that they have taken themselves, given that they post videos that they have taken themselves = 0.923