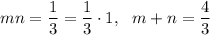Answer:
If
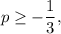 then
then
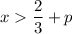 and
and
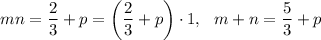
Explanation:
Solve two inequalities for x.
1.
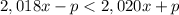
Separate terms with x and without x into two sides:
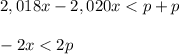
Multiply by -1:
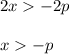
2.
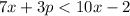
Separate terms with x and without x into two sides:
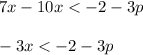
Multiply by -1:
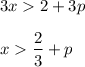
Find the largest set of x values satisfying both inequalities:
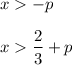
If
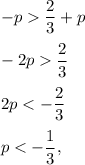
then
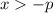 and
and
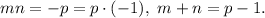 In this case both m and n are negative.
In this case both m and n are negative.
If
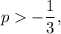 then
then
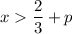 and
and
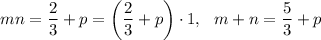
If
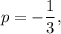 then
then
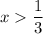 and
and