Question

In a cathode-ray tube, a beam of electrons is projected horizontally with a speed of 1.0x109 cm/s into a region between a pair of horizontal plates 2.0 cm long. An electric field between the plates causes a constant downward acceleration of the electrons of magnitude 1.0x1017 cm/s2. Find (a) the time required for the electrons to pass through the plates, (b) the vertical displacement of the beam in passing through the plates, and (c) the components of the velocity of the beam is it emerges from the plates.

Answer 1

(a)
`2\cdot 10^(-9) s`

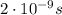
The time it takes for the electron to pass through the plates depends only on its horizontal motion,

The horizontal motion is a uniform motion, with constant velocity

`v_x = 1.0\cdot 10^9 cm/s`

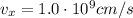
The total distance travelled by the electron to pass through the plates is

d = 2.0 cm

Using the equation for uniform motion,

`v_x = (d)/(t)`

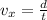
where t is the time taken. Solving for t,

`t=(d)/(v_x)=(2.0)/(1.0\cdot 10^9)=2\cdot 10^(-9) s`

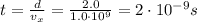
(b) -0.2 cm

The vertical motion of the electron is a uniform accelerated motion, so the vertical displacement is given by

`y=u_y t + (1)/(2)at^2`

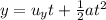
where

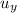`u_y` is the initial vertical velocity

`a=-1.0\cdot 10^(17) cm/s^2` is the acceleration (negative because it is downward)

We can write that

`u_y=0`

Since the electron initially travels horizontally, and so if we substitute the time we found in part (a), we can find the vertical displacement after the electron has passed through the plates:

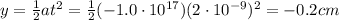
`y=(1)/(2)at^2=(1)/(2)(-1.0\cdot 10^(17))(2\cdot 10^(-9))^2=-0.2 cm`

(c)
`1.0 \cdot 10^9 cm/s, -2\cdot 10^8 cm/s`

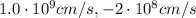
The horizontal component of the velocity of the beam does not change, since the there are no forces acting in the horizontal direction, so it remains

`v_x = 1.0 \cdot 10^9 cm/s`

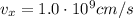
Instead, the vertical component of the velocity changes according to the equation

`v_y = u_y + at`

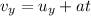
And substituting the values we found for a and t, we find

`v_y = 0 + (-1.0\cdot 10^(17))(2\cdot 10^(-9))= -2\cdot 10^8 cm/s`

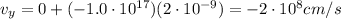
where the negative sign indicates the downward direction.