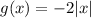Answer:
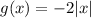
Explanation:
When a function
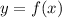 is reflected over x-axis then it actually flip itself around x-axis and gives a mirror image of the original function.
is reflected over x-axis then it actually flip itself around x-axis and gives a mirror image of the original function.
The new function will be

Given : The graph of g(x) is obtained by reflecting the graph of
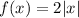 over the x-axis.
over the x-axis.
Then , g(x) should be

Therefore, the equation describes g(x) would be