ANSWER:
Standard deviation of 2, 4, 7, 8, 9 is 2.6
SOLUTION:
Given, data set is 2, 4, 7, 8, 9.
We know that, Standard deviation is given by
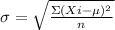
Where,
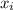 is element of data set
is element of data set
 is mean of data set
is mean of data set
n is total number observations.
Now, mean is given by
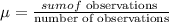
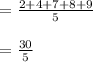
= 6
So, the mean of data set is 6.
Now, standard deviation,
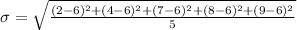
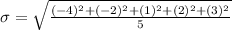
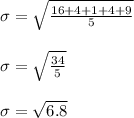
So, the standard deviation is 2.607 approximately.
When rounded to nearest tenth answer is 2.6