Question

If $800 is deposited in an account paying 7% annual interest, compounded continuously, how long will it take for the account to increase to $1300? Round your answer to the nearest hundredth of a year

Answer 1

$800 will become $ 1300 in 6.94 years when compounded continuously at the annual interest rate of 7%.

Solution:

Given that

Amount deposited = $800,

Rate if interest = 7% = 0.07

Required amount = $1300

And most important thing that interest is compounded continuously.

Formula of Amount where interest is compounded continuously is as follows

`A=P e^{\mathrm{rt}}`

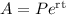
Where A is final amount,

P is principal Amount,

r = rate of interest

t = duration in years

In our case A = $1300, P = $800, r = 0.07. We need to evaluate “t” that is number of year.

On substituting given values in formula of amount we get

`1300=800 e^(0.07 t)`

`(1300)/(800) = \mathrm{e}^{0.07 \mathrm{t}}`

`1.625=\mathrm{e}^{0.07 \mathrm{t}}`

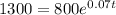
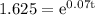
Taking ln both the sides

`\ln (1.625)=(0.07 \mathrm{t}) \ln ^(e)`

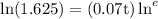
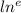`l n^(e)` = 1 .So we get,

ln(1.625) = 0.07t

`t = (ln 1.625)/(0.07)`

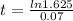
= 6.9358 ≈ 6.94 years

Hence $800 will become $ 1300 in 6.94 years when compounded continuously at the annual interest rate of 7%.