Answer:
Answered
Explanation:
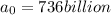
r= 1.12%= 0.0112
a) let a_n represents population n years after 2017
each year population grows by 1.12 %. Thus the population is the population of the previous year multiplied by a factor of 1.12%.
that is
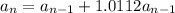
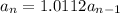
b) given
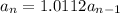
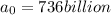
we successively apply the recurrence relation:
a_n= 1.0112a_n-1 = 1.0112^1a_n-1
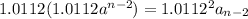
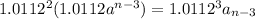
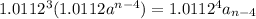
.......................
=1.0112^na_n-n
=7.6×1.0112^n
c) the population of the world be in 2050
n=33 years
=7.6×1.0112^33
=10.975 billion