Question

Assume that the population of the world in 2017 was 7.6 billion and is growing at the rate of 1.12% a year. a) Set up a recurrence relation for the population of the Links world n years after 2017. b) Find an explicit formula for the population of the world n years after 2017. c) What will the population of the world be in 2050?

Answer 1

Answered

Explanation:

`a_0= 736 billion`

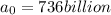
r= 1.12%= 0.0112

a) let a_n represents population n years after 2017

each year population grows by 1.12 %. Thus the population is the population of the previous year multiplied by a factor of 1.12%.

that is

`a_n =a_(n-1) +1.0112a_(n-1)`

`a_n =1.0112a_(n-1)`

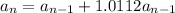
b) given
`a_n =1.0112a_(n-1)`

`a_0= 736 billion`

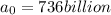
we successively apply the recurrence relation:

a_n= 1.0112a_n-1 = 1.0112^1a_n-1

`1.0112(1.0112a^(n-2))= 1.0112^2 a_(n-2)`

`1.0112^2(1.0112a^(n-3))= 1.0112^3 a_(n-3)`

`1.0112^3(1.0112a^(n-4))= 1.0112^4 a_(n-4)`

.......................

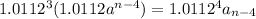
=1.0112^na_n-n

=7.6×1.0112^n

c) the population of the world be in 2050

n=33 years

=7.6×1.0112^33

=10.975 billion

Answer 2

a)
`= 1.0112 a_(n-1)`

b)
`= 7.6 . 1.0112^n`

c)
`a_(33) = 10.97 billion`

Explanation:

Given data:

Population in 2017 was 7.6 billion

r = 1.12%

a) population after n year 2017

It is given each year population rise at a rate of 1.12% Thus we have

`a_n = a_(n-1) + 1.12%.a_(n-1)`

`= a_(n-1) + 0.0112 a_(n-1)`

`= 1.0112 a_(n-1)`

b)
`a_(n)  = 1.0112 a_(n-1)`

`a_(n)  = 1.0112 a_(n-1) = 1.011 ^1 a_(n-1)`

`a_(n)  = 1.0112 a_(n-2) = 1.011 ^2 a_(n-2)`

`a_(n)  = 1.0112 a_(n-3) = 1.011 ^3 a_(n-3)`

....

`= 1.0112^n a_(n-n)`

`= 1.0112^n a_(0)`

`= 7.6 . 1.0112^n`

c) for n = 33 year ( 2050- 2017 = 33 year)

`a_(33) = 7.6 * 1.0112^33`

`a_(33) = 10.97 billion`