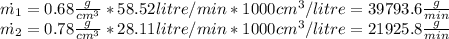Answer:
Density of final mixture=0.7175
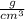 . Mass/Volumetric flow rate stream 1= 39793.6
. Mass/Volumetric flow rate stream 1= 39793.6
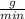 / 58.52 litre/min. Mass/Volumetric flow rate stream 2= 21925.8
/ 58.52 litre/min. Mass/Volumetric flow rate stream 2= 21925.8
 / 28.11 litre/min
/ 28.11 litre/min
Step-by-step explanation:
The first thing to do is the density's determination. For this you can establish a system of equation. For stream 1, you know that 10%wt of ethanol + 90%wt hexane give a density of 0.68
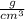 . Calling "X" to the ethanol's density and "Y" Hexane`s one:
. Calling "X" to the ethanol's density and "Y" Hexane`s one:
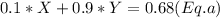
The same applies to stream 2,so:
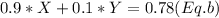
Solving: X=0.7925
 ; Y= 0.6675
; Y= 0.6675
 .
.
Then, since the final concentration is 40%wt ethanol and 60%wt hexane, the density of the final mixture is:
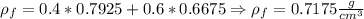
Then, you know the volume of the tank (500gallons=1892500cm^3), the density (0.7175 g/cm^3) and mixture (40%wt ethanol;60%hexane). From here you can get the mass of each gas in the tank.
Mass of ethanol=0.4*1892500* 0.7175 g=543147.5 g (grams)
Mass of hexane=0.6*1892500* 0.7175 g=814721.25 g (grams)
These masses come from both stream so it is necessary to know the net volume from each stream. For this, the following equation are needed.
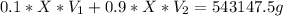 (Mass of ethanol)
(Mass of ethanol)
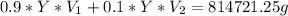 (Mass of hexane)
(Mass of hexane)
Solving, the volume from stream 1 (
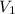 ) is 1287528.15 cm^3 and the volume from stream 2 (
) is 1287528.15 cm^3 and the volume from stream 2 (
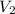 ) is 618452.00 cm^3.
) is 618452.00 cm^3.
Then, the time for complete the tank is 22 min, so the volume rate is:
For stream 1:

For stream 2:
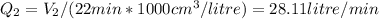
Finally, multiplying the volume rate by the density of each current the mass flow is: