Question

Naturally occurring silicon has an atomic mass of 28.086 and consists of three isotopes. The major isotope is 28Si, natural abundance 92.23%, relative atomic mass 27.97693. The next most abundant isotope is 29Si, relative atomic mass 28.97649. The third isotope is 30Si whose natural abundance is in the ratio of 0.6592 to that of 29Si.

Answer 1

The average atomic mass of silicon can be calculated by considering the natural abundance of its isotopes and their respective masses. Calculation for silicon gives an average atomic mass of approximately 28.08553 amu.

Step-by-step explanation:

To find the average atomic mass of an element with multiple isotopes, you need to consider the mass of each isotope and its natural abundance. In the case of silicon, there are three isotopes: 28Si, 29Si, and 30Si. The first step is to convert the natural abundances to a ratio. Given that the natural abundance of 30Si is in the ratio of 0.6592 to that of 29Si, we can assume that the natural abundance of 29Si is 1.0000.

Calculating the sum of the isotopes' masses multiplied by their respective natural abundances will give us the average atomic mass. Using the given information, we can calculate:

(27.97693 * 0.9223) + (28.97649 * 1.0000 * 0.6592) + (30.0 * 1.0000 * 0.3408) = 28.08553 amu

Therefore, the average atomic mass of silicon is approximately 28.08553 amu.

Answer 2

29Si has a natural abundance of 4.68%.

30Si has a relative atomic mass of 29.99288 and a natural abundance of 3.09%.

Step-by-step explanation:

The atomic mass of silicon is given by:

Si=Si²⁸×A₁+Si²⁹×A₂+Si³⁰×A₃

Where:

Si: atomic mass of silicon (28.086)

Si²⁸: relative atomic mass of 28Si (27.97693)

A₁: natural abundance of 28Si (92.23%)

Si²⁹: relative atomic mass of 29Si (28.97649)

A₂: natural abundance of 29Si

Si³⁰: relative atomic mass of 30Si

A₃: natural abundance of 30Si

We also know that 30Si natural abundance is in the ratio of 0.6592 to that of 29Si.

We have to set up a system of three equations in three unknowns:

Si=Si²⁸×A₁+Si²⁹×A₂+Si³⁰×A₃

A₃=0.6592×A₂

A₁+A₂+A₃=1

First, we find substitute the value of A₃ in the third equation and solv teh value of A₂:

A₁+A₂+0.6592×A₂=1

A₁+1.6592×A₂=1

1.6592×A₂=1-A₁

A₂=
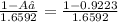`(1-A₁)/(1.6592)=(1-0.9223)/(1.6592)`=0.0468

Then, we find the value of A₃:

A₃=0.6592×A₂

A₃=0.6592×0.0468=0.0309

Finally, we find the value of Si³⁰ in the first equation:

Si=Si²⁸×A₁+Si²⁹×A₂+Si³⁰×A₃

28.086=27.97693×0.9223+28.97649×0.0468+Si³⁰×0.0309

28.086=27.15922+Si³⁰×0.0309

28.086-27.15922=Si³⁰×0.0309

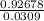`(0.92678)/(0.0309)`=Si³⁰

Si³⁰=29.99288