Question

The convection coefficient for flow over a solid sphere may be determined by submerging the sphere, which is initially at 25 °C, into the flow, which is at 75 °C, and measuring its surface temperature at some time during the transient heating process. If the sphere has a diameter of 0.1 m, a thermal conductivity of 22 W/(m·K), and a thermal diffusivity of 0.40 ×10-5 m2/s, at what time will a surface temperature of 60 ºC be recorded if the convection coefficient is 300 W/(m2·K)?

Answer 1

t = 59.37 s

Step-by-step explanation:

Given data:

thermal diffusivity
`= \alpha = (k)/(\rho c_p) =0.40* 10^(-0.5)`

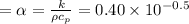
theraml conductivity = k = 22 W/m.K

h = 300 W/ m^2.K

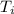`T_i` = 25 degree C = 298 k

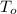`T_o` = 60 degree C = 333 k

`T_(\infty)`= 75 degree C = 348 L

diameter d = 0.1 m

characteristics length Lc = r/3 = = 0.0166

`Bi = (hLc)/(K) = (300* 0.0166)/(22) = 0.226`

`\tau = (\alpha t)/(lc^2) = (0.4* 10^(-5)* t)/(0.0166^2)`

`\tau = 0.036 t`

`(T_o -T_(\infty))/(T_i -T_(\infty)) = Ae^[\lambda^2 \tau}`

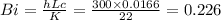
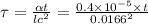
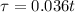
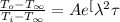
at Bi = 0.226

Ai = 0.982

`\lambda = 0.876`

`(333348)/(298-348) = 0.982e^(-0.879^2 0.036t)`

`0.3 = 0.982 e^(-0.2t)`

`0.305 = e^(-0.2t)`

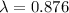
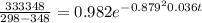
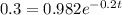
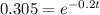
-1.187 = - 0.02t

t = 59.37 s