Question

A boy throws a baseball onto a roof and it rolls back down and off the roof with a speed of 4.05 m/s. If the roof is pitched at 40.0° below the horizon and the roof edge is 4.90 m above the ground, find the time the baseball spends in the air and the horizontal distance from the roof edge to the point where the baseball lands on the ground.

Answer 1

Step-by-step explanation:

It is given that,

Initial speed of the ball, u = 4.05 m/s

The roof is pitched at an angle of 40 degrees below the horizontal

Height of the edge above the ground, h = 4.9 m

Let for t time the baseball spends in the air. It can be solved using the second equation of motion as :

`h=ut+(1)/(2)gt^2`

`h=u\ sin\theta t+(1)/(2)gt^2`

`4.9=4.05\ sin(40)t+(1)/(2)* 9.8 t^2`

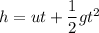
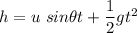
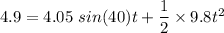
On solving the above equation, we get, t = 0.769 seconds

Let x is the horizontal distance from the roof edge to the point where the baseball lands on the ground. It can be calculated as :

`x=u\ cos\theta* t`

`x=4.05\ cos(40)* 0.769`

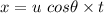
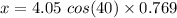
x = 2.38 meters

Hence, this is the required solution.