Question

The convection coefficient for flow over a solid sphere may be determined by submerging the sphere, which is initially at 25 °C, into the flow, which is at 75 °C, and measuring its surface temperature at some time during the transient heating process. If the sphere has a diameter of 0.1 m, a thermal conductivity of 22 W/(m·K), and a thermal diffusivity of 9.0 ×10-5 m2/s, at what time will a surface temperature of 60 ºC be recorded if the convection coefficient is 300 W/(m2·K)?

Answer 1

t= 17 .1 s

Step-by-step explanation:

Given that

Ti= 25 C

T∞= 75°C

T= 60 ºC

K=22 W/(m·K),

`h=300 W/m^2.k`

`\alpha = 9* 10^(-5)\ m^2/s`

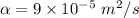
d= 0.1 m

So for sphere

Lc= d/6 = 0.0166 m

We know that

`Bi=(hL_c)/(K)`

`Bi=(300* 0.0166)/(22)`

Bi = 0.22

`Fo=(\alpha t)/(L_c^2)`

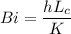
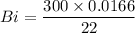
`Fo=(9* 10^(-5)*  t)/(0.0166^2)`

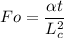
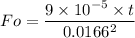
Fo = 0.32 t

Lets take

θo= Ti - T∞ =25 - 75 = 50 °C

θ = T-T∞ = 60 -75 = 15 °C

We know that

`\theta =\theta _oe^{{-Bi.Fo}}`

`15 =50e^{{-0.22* 0.32t}}`

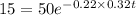
by solving this t= 17 .1 s