Answer: 0.893
Explanation:
Given : Sample size of residential water bills: n=100
Number of residences had reduced their water consumption over that of the previous year = 80
Then sample proportion:
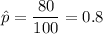
Critical value for 98% confidence=
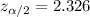
The upper bound for confidence interval for population proportion :

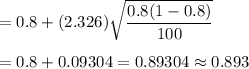
Hence, the 98% upper confidence bound for the proportion of residences that reduced their water consumption.=0.893