Answer:
(a) Magnitude of force is 262.51 N
(b) Angle with East direction is
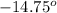
Step-by-step explanation:
Force by Jack in vector form
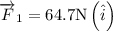
Force by Jill in Vector form is given by
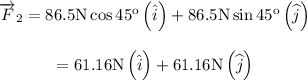
Force by Jane is
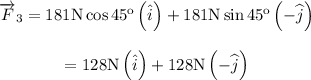
Net force is:
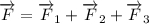
Hence
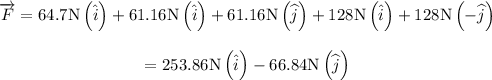
The net force will be given by
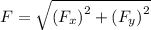
Since
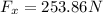 and
and
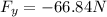
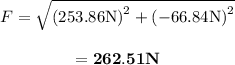
The direction of net force is:

Since
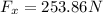 and
and
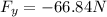
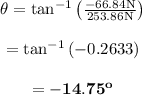
The angle with East direction is
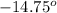
Net force exerted on the donkey is in the south-east direction. So, the angle of net force from the east direction is
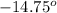 and it is
and it is
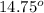 from the south.
from the south.