Answer:
-3.5
The distance Rachel covers per hour is 3.5 miles
Explanation:
After 2 hours, she is 13 miles from the campground.
After 4 hours, she is 6 miles from the campground.
Let x be the number of hours, y be the number of miles from the campground, then we have two points (2,13) and (4,6).
The equation of the line passing through the points
 and
and
 is
is
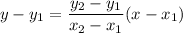
Substitute:
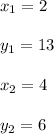
Hence,
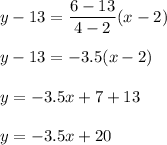
The slope of the line is
 and it represents that the distance Rachel covers per hour is 3.5 miles.
and it represents that the distance Rachel covers per hour is 3.5 miles.