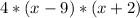Answer:
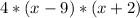
Explanation:
Start by extracting the numerical common factors. Notice that 4 is a factor in all coefficients. Therefore:
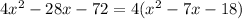
Now study the trinomial that is left, and look for numerical coefficients that multiplied give as result the last coefficient in the trinomial (-18) and when combined give you the coefficient in the linear term (-7). Notice that the coefficient -18 can be created by the product of (-9) times (2), and that these numbers combined give you exactly "-7" which is your middle coefficient. Therefore use them to factor out the trinomial:
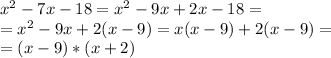
Therefore, the full factoring of the initial trinomial is written as: