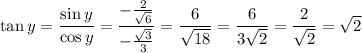Answer:

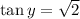
Step-by-step explanation:
Recall that
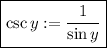
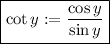
We know that
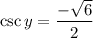
Note that according to the definition of
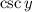 it is true that both sine and cosine are negative, once
it is true that both sine and cosine are negative, once
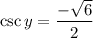 . Because
. Because
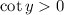 , this conclusion is true. We basically have
, this conclusion is true. We basically have
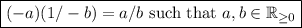
Sure it is true
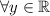 but perhaps this way is better to understand.
but perhaps this way is better to understand.
In order to find sine, we can use the definition and manipulate the rational expression.
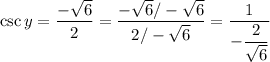
Therefore,
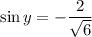
Here I just divided numerator and denominator by
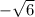 .
.
Now, to find cosine we can use the identity
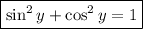
Thus,

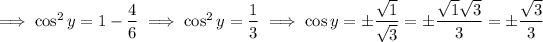
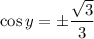
Once we have
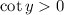 , we just consider
, we just consider

FInally, for tangent, just consider
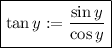
thus,