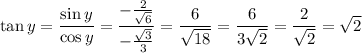Question

Find cos y and tan y if csc y = -√6/2 and cot y >0.

Answer 1

To find cos y and tan y, we can use the given information. Cos y is -√6/2 and tan y is 1/3.

Step-by-step explanation:

To find cos y and tan y, we can use the given information that csc y = -√6/2 and cot y >0. Firstly, we know that csc y is equal to 1/sin y, so if csc y = -√6/2, then sin y = -2/√6. Since cot y > 0, it means that cos y/ sin y > 0, which implies that cos y has the same sign as sin y. Therefore, cos y is negative, which gives us cos y = -√6/2. As for tan y, we can use the identity tan y = sin y/ cos y, and substitute the values we know, giving us tan y = (-2/√6)/(-√6/2) = 1/3.

Answer 2

`\cos y = -(√(3) )/(3)`

`\tan y = √(2)`

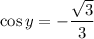
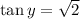
Step-by-step explanation:

Recall that

`\boxed{\csc y := (1)/(\sin y)}`

`\boxed{\cot y := (\cos y)/(\sin y)}`

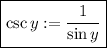
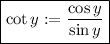
We know that

`\csc y = (-√(6) )/(2)`

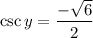
Note that according to the definition of
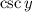`\csc y` it is true that both sine and cosine are negative, once
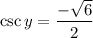`\csc y = (-√(6) )/(2)` . Because
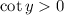`\cot y > 0`, this conclusion is true. We basically have

`\boxed{(-a)(1/-b)=a/b \text{ such that } a,b\in\mathbb{R}_(\geq 0)}`

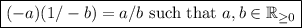
Sure it is true
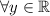`\forall y\in\mathbb{R}` but perhaps this way is better to understand.

In order to find sine, we can use the definition and manipulate the rational expression.

`\csc y = (-√(6) )/(2) = (-√(6) / -√(6) )/(2/-√(6) ) = (1 )/(-(2)/(√(6) ) )`

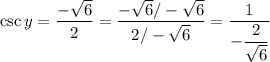
Therefore,

`\sin y =-(2)/(√(6) )`

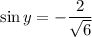
Here I just divided numerator and denominator by
`-√(6)`.

Now, to find cosine we can use the identity

`\boxed{\sin^2y +\cos ^2y =1}`

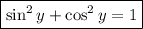
Thus,

`\left(-(2)/(√(6) )\right)^2 + \cos ^2y =1 \implies (4)/(6 ) +\cos ^2y =1`

`\implies \cos ^2y =1 - (4)/(6 ) \implies \cos ^2y =(1)/(3 ) \implies \cos y = \pm (√(1) )/(√(3) ) = \pm (√(1) √(3) )/(3) = \pm (√(3) )/(3)`

`\cos y = \pm(√(3) )/(3)`

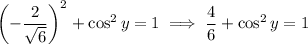
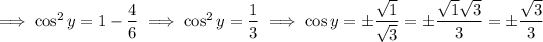
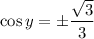
Once we have
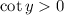`\cot y > 0`, we just consider

`\cos y = -(√(3) )/(3)`

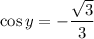
FInally, for tangent, just consider

`\boxed{\tan y := (\sin y)/(\cos y)}`

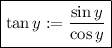
thus,

`\tan y = (\sin y)/(\cos y) = (-(2)/(√(6) ))/(-(√(3) )/(3)) = (6)/(√(18) ) =(6)/(3√(2) ) =(2)/(√(2) ) = √(2)`