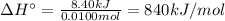Question

10. When 50.0 ml of 0.200 M AgNO3 and 50.0 ml of 0.100 M CaCl2, both at 25.0°C, are reacted in a coffee-cup calorimeter, the temperature of the reacting mixture increases to 26.0°C. Calculate ∆H in kJ per mole of AgCl produced. Assume the density of the solution is 1.05 g/ml and the specific heat capacity of the solution 4.20 J/g°C.AgNO3(aq) + HCl(aq) à AgCl(s) + HNO3(aq)

Answer 1

ΔH° = 840 kJ/mol

Step-by-step explanation:

Let's consider the following balanced reaction:

2 AgNO₃(aq) + CaCl₂(aq) ⇄ 2 AgCl(s) + Ca(NO₃)₂

Then, we need to know the moles of both reactants:

AgNO₃: n = 0.200 mol/L × 0.0500 L = 0.0100 mol

CaCl₂: n = 0.100 mol/L × 0.0500 L = 0.00500 mol

According to the balanced equation we need 2 moles of AgNO₃ per each mole of CaCl₂, and this coincides with the experimental data, so there is no limiting reactant. Let's use AgNO₃ to find out how many moles of AgCl are produced.

`0.0100molAgNO_(3).(2molAgCl)/(2molAgNO_(3)) =0.0100molAgCl`

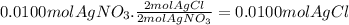
Now, we can calculate the total amount of heat released using the following expression:

Q = c × m × ΔT

where,

c is the heat capacity of the solution

m is the mass of the solution

ΔT is the change in temperature (26.0 °C - 25.0°C = 1.00 °C)

Since the volume is 100.0 mL (50.0 mL + 50.0 mL) and the density is 1.05 g/mL, we can calculate the mass of the solution like:

m = 1.05 g/mL × 100.0 mL = 105 g

Then,

`Q=c * m * \Delta T=4.20 J/g.\° C * 105 g * 1.00\° C=8.40 * 10^(3) J=8.40kJ`

Finally,

`\Delta H \° = (8.40kJ)/(0.0100mol) =840kJ/mol`