Answer:
Explanation:
Given
Probability that an inspector doe not identify low-quality timber=0.20
(a)Probability that both inspector do not identify a low quality timber
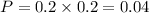
(b)Let n be the no of inspector
Probability should be less than 1%=0.01
so
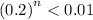
Taking
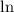 both sides
both sides
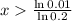
x>2.861
thus minimum value of x is 3
(c)From part b it is clear that minimum 3 officer are required to to keep the low quality timber below 1%
on an average 2 officer are not sufficient to identify 4 low quality timber out of 100