Answer:
For a: The concentration of NO at equilibrium is
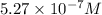
For b: The value of
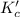 is
is
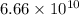
For c: The correct answer is product favored.
Step-by-step explanation:
The given chemical reaction follows:

The expression of
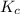 for above equation follows:
for above equation follows:
![K_c=([NO]^2)/([N_2][O_2])](https://img.qammunity.org/2020/formulas/chemistry/college/h97e3v9ia7fb0kvxd3enqoq711mg7wqk69.png)
We are given:
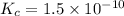
![[N_2]_(eq)=0.043M](https://img.qammunity.org/2020/formulas/chemistry/college/fihix5qy98lztzmfd73k2bi8pbszh78ybc.png)
![[O_2]_(eq)=0.043M](https://img.qammunity.org/2020/formulas/chemistry/college/bzj3nubxop2jchekak44cbbp0vixfs1t3u.png)
Putting values in above equation, we get:
![1.5* 10^(-10)=([NO]^2)/(0.043* 0.043)](https://img.qammunity.org/2020/formulas/chemistry/college/cwltrne9ygx5yefl3nqrt4cymc3nswc0d7.png)
![[NO]=\sqrt{(1.5* 10^(-15)* 0.043* 0.043)}=5.27* 10^(-7)M](https://img.qammunity.org/2020/formulas/chemistry/college/c8vkm6azlxs1yfvvqassj79qdaeq27wjrn.png)
Hence, the concentration of NO at equilibrium is
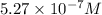
The given chemical reaction follows:
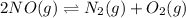
The expression of
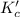 for above equation follows:
for above equation follows:
![K_c'=([N_2][O_2])/([NO]^2)](https://img.qammunity.org/2020/formulas/chemistry/college/uzt3c4raxzh1yh37fcmjn7y91py4bglnsi.png)
As, the above reaction is the reverse of equation in part a. So, the value of
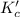 will be inverse of
will be inverse of
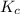
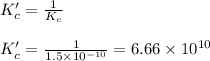
Hence, the value of
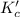 is
is
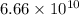
There are 3 conditions:
- When
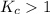 ; the reaction is product favored.
; the reaction is product favored. - When
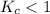 ; the reaction is reactant favored.
; the reaction is reactant favored. - When
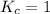 ; the reaction is in equilibrium.
; the reaction is in equilibrium.
For the reaction in part 'b', the value of
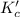 is
is
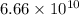
The value of
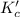 is very high than 1. So, the equilibrium in part 'b' is product favored.
is very high than 1. So, the equilibrium in part 'b' is product favored.
Hence, the correct answer is product favored.