Answer:
First we need to write the general linear function as:
F = a*C + b
Second, we use the 2 first conditions and we have as a equations:
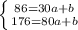
Then, resolving the system of equations, we have:
a = 1.8 and b = 32
A) So the linear function is:
F = 1.8*C + 32
B) So in this case we reverse the equation as follow:
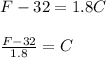
Finally we have:
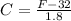
C) In this case, we consider F = C and we have:
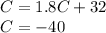
So
C = F = -40degrees