ANSWER:
The given statement
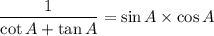 has been proved
has been proved
SOLUTION:
We need to prove that,
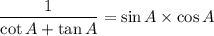
Now, take left hand side, and by solving it we have bring up the right hand side.
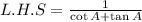
Since, we know that,
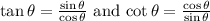
Substitute in above L.H.S we get,
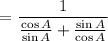
On cross- multiplication, the above expression becomes,
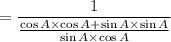
On simplification we get,
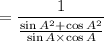
we know that the trignometric identity,
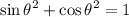 the above equation becomes
the above equation becomes
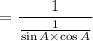
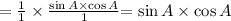
= R.H.S
L.H.S = R.H.S
Hence, the given statement has been proved.