Question

Prove that 1/cot A+ tan A=sin ACOSA​

Answer 1

I assume that means: Show

`(1)/(\cot a + \tan A) = \sin A \cos A`

Proof:

`(1)/(\cot A + \tan A)`

`= (1)/((\cos A)/(\sin A) + (\sin A)/(\cos A))`

`= (1)/((\cos^2A + \sin^2 A)/(\sin A \cos A))`

`= (\sin A \cos A)/(\cos^2A + \sin^2 A)`

`=\sin A \cos A \quad\checkmark`

Answer 2

The given statement
`$(1)/(\cot A+\tan A)=\sin A * \cos A$` has been proved

SOLUTION:

We need to prove that,
`$(1)/(\cot A+\tan A)=\sin A * \cos A$`

Now, take left hand side, and by solving it we have bring up the right hand side.

`L.H.S = (1)/(\cot A+\tan A)$`

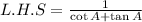
Since, we know that,
`\tan \theta=(\sin \theta)/(\cos \theta)$ and $\cot \theta=(\cos \theta)/(\sin \theta)$`

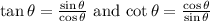
Substitute in above L.H.S we get,

`$=(1)/((\cos A)/(\sin A)+(\sin A)/(\cos A))$`

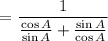
On cross- multiplication, the above expression becomes,

`$=(1)/((\cos A * \cos A+\sin A * \sin A)/(\sin A * \cos A))$`

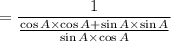
On simplification we get,

`$=(1)/((\sin A^(2)+\cos A^(2))/(\sin A * \cos A))$`

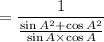
we know that the trignometric identity,
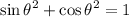`$\sin \theta^(2)+\cos \theta^(2)=1$` the above equation becomes

`$=(1)/((1)/(\sin A * \cos A))$`

`=(1)/(1) * (\sin A * \cos A)/(1)$$=\sin A * \cos A$`

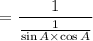
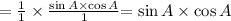
= R.H.S

L.H.S = R.H.S

Hence, the given statement has been proved.