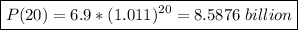Question

Assume that the population of the world in 2010 was 6.9billion and is growing at the rate of 1.1% a year. a) Set up a recurrence relation for the population of theworld n years after 2010. b) Find an explicit formula for the population of theworld n years after 2010. c) What will the population of the world be in 2030? 21. A factory makes custom sports cars at an increasing rate

Answer 1

a)

If we call P(n) the population n years after 2010, the recurrence relation for the population of the world n years after 2010 would be

P(0) = 6.9 billion

P(n) = P(n-1)*(1.011)

b)

`P(n)={6.9*(1.011)^n`

c)

`6.9*(1.011)^(20) = 8.5876\; billion`

Explanation:

a)

If the growing rate is 1.1% in the year 2011 was

6.9 + 1.1% of 6.9 = 6.9 + 6.9*(0.011) = 6.9*(1.011)

In the year 2012, the new population was

6.9*(1.011) + 1.1% of 6.9*(1.011)

= 6.9*(1.011) + 6.9*(1.011)*(0.011) = 6.9*(1.011)*(1+0.011)

= 6.9*(1.011)*(1.011) =
`6.9*(1.011)^2`

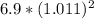
Similarly, we can see that the population in 2013 was

`6.9*(1.011)^3`

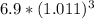
If we call P(n) the population n years after 2010, the recurrence relation for the population of theworld n years after 2010 would be

P(0) = 6.9 billion

P(n) = P(n-1)*(1.011)

b)

In the year n after 2010, the population would be

`P(n)={6.9*(1.011)^n`

c)

The population of the world in 2030, according to the formula, will be P(20)

`\boxed{P(20) = 6.9*(1.011)^(20) = 8.5876\; billion}`