Answer:
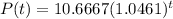
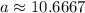

Explanation:
It is given that a population, P(t) (in millions) in year t, increases exponentially.
The given values of he function are P(9)=16 and P(18)=24.
The formula for the population in the form

where, a is the initial population and b is growth factor.
P(9)=16 means P(t)=16 at x=9.
 .... (1)
.... (1)
P(18)=24 means P(t)=24 at x=18.
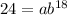 .... (2)
.... (2)
Divide equation (2) by equation (1).
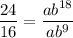

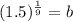

Substitute
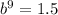 in equation (1).
in equation (1).

Divide both sides by 1.5.
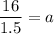
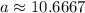
Substitute the values of a and b in the given formula.
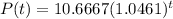
Therefore, the formula for population is
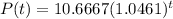 .
.