Question

Consider a plane composite wall that is composed of two materials of thermal conductivities kA = 0.1 W/m*K and kB = 0.04 W/m*K and thicknesses LA = 10 mm and LB = 20 mm. The contact resistance at the interface between the two materials is known to be 0.30 m2*K/W. Material A adjoins a fluid at 200°C for which h = 10 W/m2*K, and material B adjoins a fluid at 40°C for which h = 20 W/m2*K. (a) What is the rate of heat transfer thro

Answer 1

q=39.15 W/m²

Step-by-step explanation:

We know that

Thermal resistance due to conductivity given as

R=L/KA

Thermal resistance due to heat transfer coefficient given as

R=1/hA

Total thermal resistance

`R_(th)=(L_A)/(AK_A)+(L_B)/(AK_B)+(1)/(Ah_1)+(1)/(Ah_2)+(1)/(Ah_3)`

Now by putting the values

`R_(th)=(0.01)/(0.1A)+(0.02)/(0.04A)+(1)/(10A)+(1)/(20A)+(1)/(0.3A)`

`R_(th)=4.083/A\ K/W`

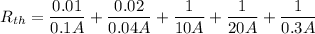
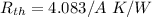
We know that

Q=ΔT/R

`Q=(\Delta T)/(R_(th))`

`Q=A* (200-40)/(4.086)`

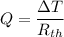
So heat transfer per unit volume is 39.15 W/m²

q=39.15 W/m²