Answer:
The second gamble has the higher expected value. EV = 4
Step-by-step explanation:
In betting, expected value can be defined as (Amount won per bet * probability of winning) – (Amount lost per bet * probability of losing)
For the first gamble:
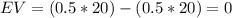
For the second gamble:
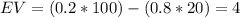
This means that Cal is expected to earn $4 for each $20 waged on the second gamble while he is expected to break even in the first gamble.
Therefore, the second gamble has the higher expected value.