Answer:
A) AB ⊥ AC
B) The triangle is a right triangle.
C) The triangle is an isosceles triangle
Explanation:
we know that
the formula to calculate the distance between two points is equal to

step 1
Find the distance AB
we have
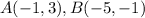
substitute in the formula
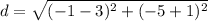
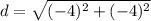
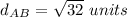
step 2
Find the distance BC
we have
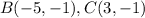
substitute in the formula
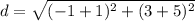
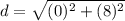
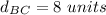
step 3
Find the distance AC
we have
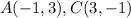
substitute in the formula
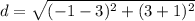
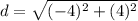
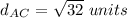
step 4
Compare the length sides of triangle
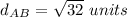
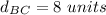
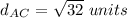
therefore
The triangle ABC is an isosceles triangle, because has two equal sides
The triangle ABC is a right triangle because satisfy the Pythagoras theorem
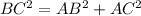
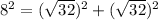
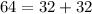
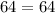 ----> is true (Is a right triangle)
----> is true (Is a right triangle)
AB ⊥ AC because in a right triangle the legs are perpendicular