Option B
ANSWER:
The factors of
 is
is
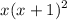
SOLUTION:
Given, cubic expression is

Now, we have to find the factors of above equation.
To factorize the given equation, follow the below steps:
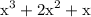
Since x is common in every term of expression, we can take it as common
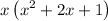
“2x” can be rewritten as “x + x”, the above equation becomes,
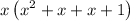
Taking the common terms out of bracket. we get
x(x (x + 1) + 1 (x + 1))
Taking (x + 1) as common., we get
x ((x + 1)(x + 1))
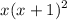
Hence, the second option b is correct.