Answer:
Option 1 -
![64^{(1)/(4)}=2\sqrt[4]{4}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pbz3om2zbkbcmgvqju3jyys1j5unfnahkz.png)
Explanation:
Given : Expression 64 Superscript one-fourth i.e.
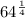
To find : Which is equivalent to expression ?
Solution :
Step 1 - Write the expression,
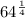
Step 2 - Factor the term 64,
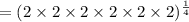
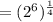
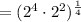
Step 3 - Apply exponent rule,
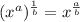
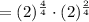
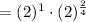
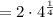
![=2\sqrt[4]{4}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/ww0q0i2l0c2p2ds4m2crd7m9zuxz90cq97.png)
Therefore,
![64^{(1)/(4)}=2\sqrt[4]{4}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pbz3om2zbkbcmgvqju3jyys1j5unfnahkz.png)
So, Option 1 is correct.