Question

Find how many terms of a geometric progression 1+3+9 are required to make a total of more than 1 million.

Answer 1

The partial sum of a geometric sequence is

`\displaystyle \sum_(i=0)^N a^i = (a^(N+1)-1)/(a-1)`

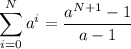
In your case a=3, so if we sum N terms of the sequence we have

`\displaystyle \sum_(i=0)^N 3^i = (3^(N+1)-1)/(2)`

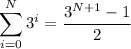
We want this to me more than 1 million, so we have

`(3^(N+1)-1)/(2)>1000000 \iff 3^(N+1)-1>2000000 \iff 3^(N+1) > 1999999`

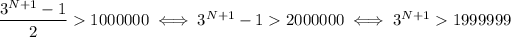
Considering the log (base 3) of both sides, we have

`N+1>\log_3(1999999)\iff N>\log_3(1999999)-1 approx 12.2`

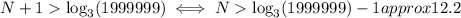
So, starting from N=13, the sum of the first N terms will be more than 1 million