The partial sum of a geometric sequence is
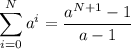
In your case a=3, so if we sum N terms of the sequence we have
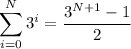
We want this to me more than 1 million, so we have
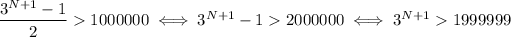
Considering the log (base 3) of both sides, we have
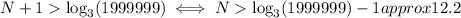
So, starting from N=13, the sum of the first N terms will be more than 1 million