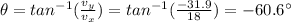Question

A person standing at the edge of a seaside cliff kicks a stone, horizontally over the edge with a velocity of 18 m/s. The cliff is 52 m above the waters surface

A. How long does it take for the stone to fall to the water
B. What is the vertical velocity component of the stone just before it hits the water
C. What is the horizontal velocity component of the stone just before it hits the water
D. What is the total velocity of the stone just before it hits the water ?

Answer 1

A) 3.26 s

To find the time of flight, we can just analyze the vertical motion of the stone. The vertical displacement is given by

`y=u_y t - (1)/(2)gt^2`

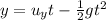
where

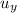`u_y` is the initial vertical velocity

t is the time

`g=9.8 m/s^2` is the acceleration of gravity

In this problem we have

y = -52 m (vertical displacement)

`u_y=0` (the stone is kicked horizontally, so it has no initial vertical velocity)

Solving for t, we find the time of flight:

`y=-(1)/(2)gt^2\\t=\sqrt{(-2y)/(g)}=\sqrt{(-2(-52))/(9.8)}=3.26 s`

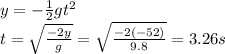
B) -31.9 m/s

The vertical velocity component at time t is given by the equation

`v_y = u_y -gt`

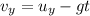
where

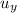`u_y` is the initial vertical velocity

t is the time

`g=9.8 m/s^2` is the acceleration of gravity

As we said previously,

`u_y = 0`

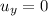
So if we substitute t = 3.26 s (time of flight), we find the vertical velocity when the stone reaches the water:

`v_y = 0 - (9.8)(3.26)=-31.9 m/s`

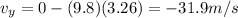
where the negative sign means the direction is downward.

C) 18 m/s

In a projectile motion, the horizontal motion is a uniform motion: since there are no forces acting on the projectile along the horizontal direction, the horizontal acceleration is zero, and so the horizontal velocity is constant.

The stone has been initially kicked with an horizontal velocity of

`v_x = 18 m/s`

So the horizontal velocity just before it hits the water is still 18 m/s.

D) 36.6 m/s at
`-60.6^(\circ)`

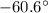
The total velocity of the stone just before it hits the water is given by:

`v=√(v_x^2+v_y^2)`

where previously we found that

`v_x = 18 m/s\\v_y = -31.9 m/s`

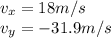
Substituting,

`v=√(18^2+(-31.9)^2)=36.6 m/s`

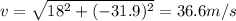
And the direction is

`\theta=tan^(-1)((v_y)/(v_x))=tan^(-1)((-31.9)/(18))=-60.6^(\circ)`