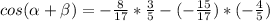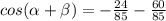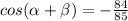Answer:
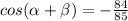
Explanation:
we know that
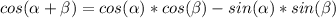
Remember the identity
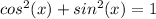
step 1
Find the value of
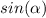
we have that
The angle alpha lie on the III Quadrant
so
The values of sine and cosine are negative
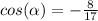
Find the value of sine
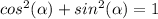
substitute
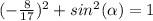
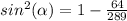
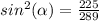
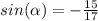
step 2
Find the value of
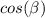
we have that
The angle beta lie on the IV Quadrant
so
The value of the cosine is positive and the value of the sine is negative
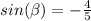
Find the value of cosine
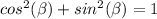
substitute
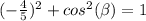
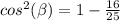
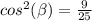
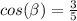
step 3
Find cos (α + β)
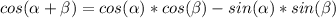
we have
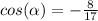
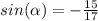
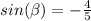
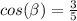
substitute